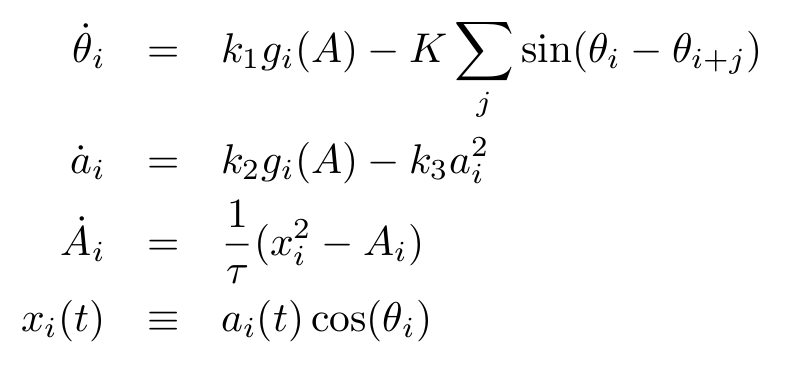Formulating a Feature Extractor Feedback System as an Ordinary Differential Equation

The basic idea of a Feature Extractor Feedback System (FEFS) is to have an audio signal generator whose output is analysed with some feature extractor, and this time varying feature is mapped to control parameters of the signal generator in a feedback loop.

What would be the simplest possible FEFS that still is capable of a wide range of sounds? Any FEFS must have the three components: a generator, a feature extractor and a mapping from signal descriptors to synthesis parameters. As for the simplicity of a model, one way to assess it would be to formulate it as a dynamic system and count its dimension, i.e. the number of state variables.

Although FEFS were originally explored as discrete time systems, some variants can be designed using ordinary differential equations. The generators are simply some type of oscillator, but it may be less straightforward to implement the feature extractor in terms of ordinary differential equations. However, the feature extractor (also called signal descriptor) does not have to be very complicated.

One of the simplest possible signal descriptors is an envelope follower that measures the sound's amplitude as it changes over time. An envelope follower can be easily constructed using differential equations. The idea is simply to appy a lowpass filter (as described in a previous post) to the squared input signal.

For the signal generator, let us consider a sinusoidal oscillator with variable amplitude and frequency. Although a single oscillator could be used for a FEFS, here we will consider a system of N circularly connected oscillators.

The amplitude follower introduces slow changes to the oscillator's control parameters. Since the amplitude follower changes smoothly, the synthesis parameters will follow the same slow, smooth rhythm. In this system, we will use a discontinuous mapping from the measured amplitudes of each oscillator to their amplitudes and frequencies. To this end, the mapping will be based on the relative measured amplitudes of pairs of adjacent oscillators (remember, the oscillators are positioned on a circle).

Let g(A) be the mapping function. The full system is

with control parameters k₁, k₂, k₁, K and τ. The variables θ are the oscillators' phases, a are the amplitude control parameters, A is the output of the envelope follower, and x(t) is the output signal. Since x(t) is an N-dimensional vector, any mixture of the N signals can be used as output.

Let the mapping function be defined as

where U is Heaviside's step function and b_j is a set of coefficients. Whenever the amplitude of an oscillator grows past the amplitude of its neighboring oscillators, the value of the functions g changes, but as long as the relative amplitudes stay within the same order relation, g remains constant. Thus, with a sufficiently slow amplitude envelope follower, g should remain constant for relatively long periods before switching to a new state. In the first equation which governs the oscillators' phases, the g functions determine the frequencies together with a coupling between oscillators. This coupling term is the same as is used in the Kuramoto model, but here it is usually restricted to two other oscillators. The amplitude a grows at a speed determined by g but is kept in check by the quadratic damping term.

Although this model has many parameters to tweak, some general observations can be made. The system is designed to facilitate a kind of instability, where the discontinuous function g may tip the system over in a new state even after it may appear to have settled on some steady state. Note that there is a finite number of possible values for the function g: since U(x) is either 0 or 1, the number of distinct states is at most 2^N for N oscillators. (The system's dimension is 3N; the x variable in the last equation is really just a notational convenience.)

There may be periods of rapid alteration between two states of g. There may also be periodic patterns that cycle through more than two states. Over longer time spans the system is likely to go through a number of different patterns, including dwelling a long time in one state.

Let S be the total number of states visited by the system, given its parameter values and specific initial conditions. Then S/2^N is the relative number of visited states. It can be conjectured that the relative number of states visited should decrease as the system's dimension increases. Or does it just take much longer time for the system to explore all of the available states as N grows?

The coupling term may induce synchronisation between the oscillators, but on the other hand it may also make the system's behaviour more complex. Without coupling, each oscillator would only be able to run at a discrete set of frequencies as determined by the mapping function. But with a non-zero couping, the instantaneous frequencies will be pushed up or down depending on the phases of the linked oscillators. The coupling term is an example of the seemingly trivial fact that adding structural complexity to the model increases its behavioural complexity.

There are many papers on coupled systems of oscillators such as the Kuramoto model, but typically the oscillators interact through their phase variables. In the above model, the interaction is mediated through a function of the waveform, as well as directly between the phases through the coupling term. Therefore the choice of waveform should influence the dynamics, which indeed has been found to be the case.

With all the free choices of parameters, of the b coefficients, the waveform and the coupling topology, this model allows for a large set of concrete instantiations. It is not the simplest conceivable example of a FEFS, but still its full description fits in a few equations and coefficients, while it is capable of seemingly unpredictable behaviour over very long time spans.

Manifesto for self-generating patches

Ideas for the implementation of autonomous instruments in analog modular synths (v. 0.2)

The following guidelines are not meant as aesthetic value judgements or prescriptions as to what people should do with their modulars — as always, do what you want! The purpose is to propose some principles for the exploration of a limited class of patches and a particular mode of using the modular as an instrument.

Self-generating patches are those which, when left running without manual interference, produce complex and varied musical patterns. Usually, the results will be more or less unpredictable. In this class of patches, there are no limitations as to what modules to use and how to connect them, except that one should not change the patch or touch any knobs after the patch has been set up to run. An initial phase of testing and tweaking is of course allowed, but if preparing a recording as documentation of the self-generating patch, it should just run uninterrupted on its own.

A stricter version of the same concept is to try to make a deterministic autonomous system in which there is no source of modulation (such as LFOs or sequencers) that is not itself modulated by other sources. In consequence, the patch has to be a feedback system.

The patch may be regarded as a network with modules as the nodes and patch cords as the links. Specifically, it is a bidirectional graph, because modules usually have both inputs and outputs. (The requirement that there be no source of modulation which itself is not modulated by other modules implies that, e.g., noise modules or LFOs without any input are not allowed.) Thus, in the graph corresponding to the patch, each node that belongs to the graph must have at least one incomming link and at least one outgoing link. The entire patch must be interconnected in the sense that one can follow the patch cords from any module through intervening modules to any other module that belongs to the patch.


Criterion of elegance:
The smaller the number of modules and patch cords used, the more elegant the patch is. (Caveat: modules are not straightforwardly comparable. There are small and simple modules with restricted possibilities, and modules with lots of features that may correspond to using several simpler modules.)

Aesthetic judgement:
Why not organize competitions where the audience may vote for their favourite patches, or perhaps let a panel of experts decide.

Standards of documentation:
Make a high quality audio recording with no post processing other than possibly volume adjustment. Video recordings and/or photos of the patch are welcome, but a detailed diagram explaining the patch and settings of all knobs and switches involved should be submitted. The diagram should provide all the information necessary to reconstruct the patch.

Criterion of robustness:
Try to reconstruct the patch with some modules replaced by equivalent ones. Swap one oscillator for another one, use a different filter or VCA and try to get a similar sound. Also try small adjustments of knobs and see whether it affects the sound in a radical way. The more robust a patch is, the easier it should be for other modular enthusiasts to recreate a similar patch on their system.

Criteria of objective complexity:
The patch is supposed to generate complex, evolving sounds, not just a static drone or a steady noise. Define your own musical complexity signal descriptor and apply it to the signal. Or use one of the existing complexity measures.

Dissemination:
Spread your results and let us know about your amazing patch!

How to patch your own oscillator

The charming world of analog modular synthesis offers many choices regarding how to construct one's instrument from components. There are lots of oscillators, filters, VCAs, LFOs, signal processors and utility modules to choose among. In that setting, it can be very interesting to build something as elementary as an oscillator out of even more basic components. Here is an example of how it can be done with two modules, neither of which functions as an oscillator on its own.

The modules needed are a utility module that mixes, offsets and inverts signals, and a dual slew limiter (or two separate slew limiters). In particular, this example will work with Doepfer's Slew Limiter A-170 SL and wmd's Invert Offset mk II. However, there is nothing magic about these modules, so other modules that offer equivalent functionality may replace them.

Five patch cords are needed to connect the modules as illustrated. Then, with some tweaking of the knobs, slow oscillations should occur. It is possible to influence the frequency by the settings of all the knobs. By adjusting the two lower knobs of A-170, controlling the rise and fall times, the wave shape can also be varied from rising ramp through triangle to falling ramp. The amplitude may be low, and the frequency usually sub-audio, although low bass frequencies in the audio range can be obtained. The effects are best observed if the CV out of the Invert Offset is routed to the frequency input of another oscillator.

What is actually going on in this patch? To a first approximation, the slew limiter can be regarded as an integrator. In fact, it is probably more accurate to think of it as a leaky integrator. The Invert Offset consists of two identical blocks with two signal inputs and two outputs each. Let us introduce the labels x₊, x_-, y₊ and y_- for the output signals, and u_x, u_y, v_x and v_y for the inputs, as shown in the sketch above. The knobs, labeled c_x and c_y, add a constant offset to the signal. Inferring from the user's manual, the following set of equations should describe what the module does.

Expressing the action of the slew limiter as an integral, and following the patch cords that go into the inputs of the Invert Offset module, the system is given by:

After a number of substitutions, and taking derivatives to get rid of the integrals, the system simplifies to:

If the constants are both zero, the eigenvalues of this system are 1±i, indicating that the system is unstable. Clearly something in the model is wrong, since the actual patch does not blow up in any way. As hinted at earlier, the slew limiters do not actually integrate the signal. If they did, there would be infinite gain at dc so any constant signal fed into one of them would keep increasing linearly. What happens in reality is that, starting from a relaxed state and feeding a constant signal into a slew limiter, the output grows from zero until it reaches the level of the input. If one had two true integrators and an inverter, the equations for an harmonic oscillator

could be realized quite easily. 

The moral of this failed attempt at modeling two quite simple modules is that even seemingly simple modules may hide more complex behaviour than one would naively suspect. In any case, it may be surprising to find that five patch cords connecting these modules in the right way are all it takes to turn them into a low frequency oscillator. Although there are more than one way to patch up an oscillator from these two modules, there are many more ways to patch up systems that do not oscillate. Bistable systems with hysteresis is the result in most cases.

Feedback FM with bells and whistles

Single oscillator feedback FM is a most economic technique for producing rich harmonic tones. However, the technique suffers from parasitic oscillations at the Nyquist frequency when the modulation index is turned up sufficiently high. The most obvious thing to try is to modify the original formula

x[n] = sin(ωn + Ix[n-1])

by lowpass filtering the feedback signal with some filter that has a zero at half the sample rate. A two point average increases the range the index can take before the spurious oscillations set in, but it cannot stop them at sufficiently high modulation indices. A complementary trick is to put a filter outside the feedback loop. Again, it helps to a certain extent, but should not be expected to solve the problem in all cases. Finally, there is the Overkill Solution of oversampling the system. Or maybe it's not so overkill after all. In any case, a high sample rate is recommended.

Feedback FM waveform with spurious oscillations and no attempt to squelch them.

Depending on the sample rate, the spurious oscillations will typically ring at such a high frequency that only domestic animals will notice them and possibly object to their presence. Nonetheless, the waveform will be contaminated by a conspicuous wiggle that may annoy any purist, whether or not they hear it. Of course, it is a spurious or parasitic oscillation since it follows the sampling rate rather than the synthesis parameters. Sometimes the parasitic oscillation happens at a third or fourth of the sample rate, or other subharmonics.

Single oscillator feedback FM is limited to harmonic spectra. Much flexibility is gained  by introducing a second oscillator since there are several ways to connect the two oscillators. Rather than listing all cases separately, we introduce coupling parameters c (cross terms) and b (self-modulation) in the coupled system

      x[n+1] = sin(θ[n] + b₁x[n] + c₁y[n])

(*)   y[n+1] = sin(φ[n] + b₂y[n] + c₂x[n])

where the phases θ and φ are incremented by the modulating and carrier frequencies. Which one is which depends on what signal you send to the output. Of course both signals can be used for stereo, but then it makes less sense to call one of the oscillators the carrier and the other one the modulator.

In FM synthesis, the phase variables usually depend only on their respective frequencies. By introducing an interaction term, phase coupling can be used to synchronize the oscillators. Hardsync may have been used with FM before, but the gentler kind of sync used in the Kuramoto model is useful here, as it is also suitable for synchronizing more than two oscillators. Now, the phases are incremented by the oscillators' frequencies as usual, but to that we add a coupling term with strength K:

      θ[n+1] = θ[n] + ω_c - K sin(θ[n] - φ[n])
(#)   φ[n+1] = φ[n] + ω_m - K sin(φ[n] - θ[n])

Turning up K too much will collapse the two oscillators into a single strong team working in perfect sync. The system (*, #) is just a four-dimensional map with seven parameters and may thus be studied with the appropriate methods of dynamic systems.

As often happens with iterated maps, the feedback FM system exhibits typical behaviour such as period two oscillations, and the period doubling route to chaos. The frequency terms may both be set to zero, which means the system (*) becomes autonomous. Then period doublings can be seen more easily, as shown below. The system has to be seeded with nonzero initial values for any oscillation to occur.

Colour legend: gray, period 1; orange, period 2; blue, period 4, bright yellow, period 3, red, chaos. On the horizontal axis, -1 < c₁ = c₂ < 4, vertical axis: - 0.5 < b₁ < 5 and b₂ = 0.5 (constant). The modulator and carrier frequencies are both 0; hence the coupling term does not influence the dynamics.

We are not done with feedback FM!

Other things to try include modifying the feedback signals by waveshapers and filters. Even the phase coupled signal may be filtered. Each filter adds its state variables to the system and increases its dimension. This is complicated territory; suffice it to say that filters plus strong nonlinearities or high feedback gain equals noise!